Integration

Intuition §

Intuitively, the integral of a function is the area under the curve. Let’s try approximating it.

First, we define

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Partition”,“label”:“partition”,“_index”:0}] Definition 1 (Partition). A partition of $[a,b]$ is a collection of points $t_0=a<t_1<t_2<\cdots <t_{n-1}<b=t_n$.

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Step Function”,“label”:“step-function”,“_index”:1}] Definition 2 (Step Function). A function $S$ defined on $[a,b]$ is a step function if there is a partition $P$ and constants $c_1,\dots ,c_n$ s.t. $S(x)=c_j$ for $x\in [t_{j-1},t_j)$ and $S(t_n)=c_n$.

If we approximate a function as a step function for a given partition, we get that the integral is

$${\int }_a^{b}S(x)dx=\sum _{j=1}^n{c}_j(t_j-t_{j-1}).$$

This approximation is a Riemann sum. It is equivalent to splitting up the area under the curve as rectangles, and then summing the areas of the rectangles.

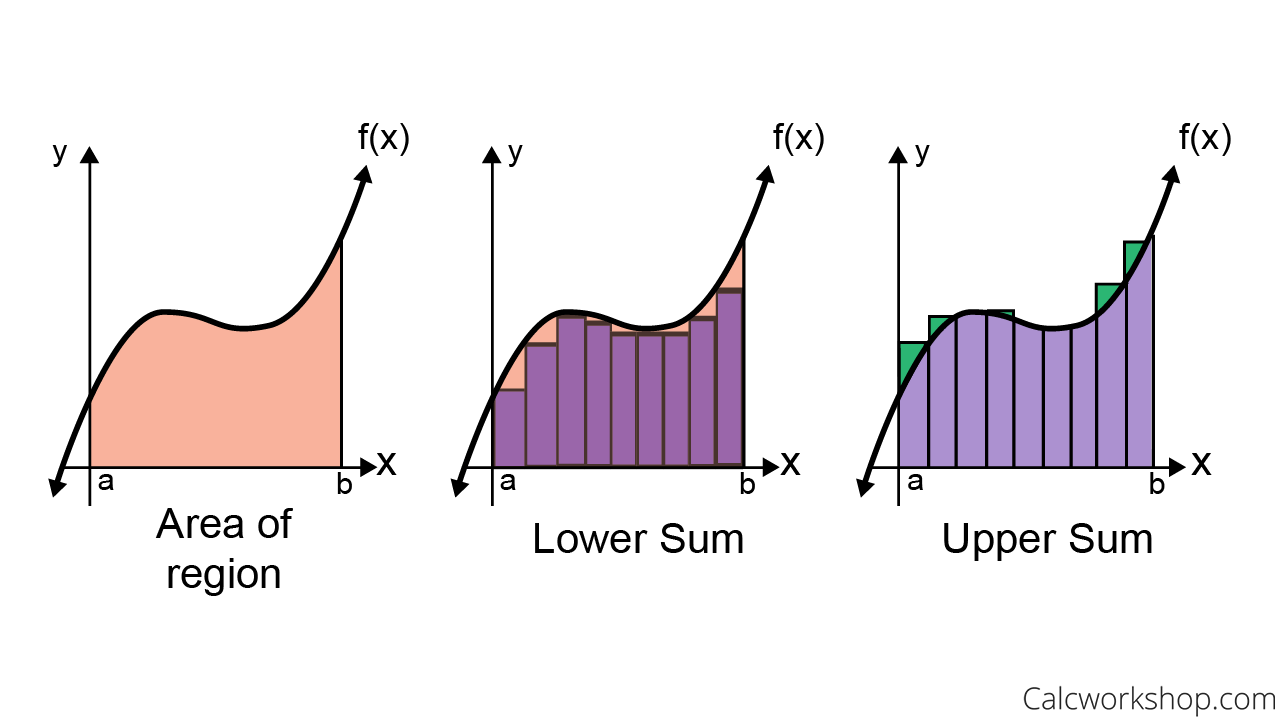
If we choose $c_j={\text{inf}}_f([t_{j-1},t_j])$, where ${\text{inf}}_f$ is the infimum of the function $f$ for a given interval, then we get the lower Riemann Sum:

$$L(f,P)=\sum _{j=1}^n{\text{inf}}_f([t_{j-1},t_j])\cdot (t_j-t_{j-1})$$

If we choose $c_j={\text{sup}}_f([t_{j-1},t_j])$, then we get the upper Riemann Sum:

$$U(f,P)=\sum _{j=1}^n{\text{sup}}_f([t_{j-1},t_j])\cdot (t_j-t_{j-1})$$

Formal Definition §

To define integration formally, we need more definitions.

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Refinement”,“label”:“refinement”,“_index”:2}] Definition 3 (Refinement). If $P,P^{\prime }$ are partitions of $[a,b]$, $P^{\prime }$ is a refinement of $P$ iff the set of points in $P$ is contained in the sets of points in $P^{\prime }$.

Note that $P,P^{\prime }$ have a common refinement $P^{\prime \prime }$. Considering common refinements, we can show that the sum and product of step functions are step functions.

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Span”,“label”:“span”,“_index”:3}] Definition 4 (Span). If $f$ is bounded on $[a,b]$, its span is ${\text{span}}_f([a,b])=\text{sup}([a,b])-{\text{inf}}_f([a,b])$, where ${\text{sup}}_f$ and ${\text{inf}}_f$ are the supremum and infimum.

Now, we can define

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Integrable”,“label”:“integrable”,“_index”:4}] Definition 5 (Integrable). A bounded function $f$ on $[a,b]$ is integrable iff for every $ϵ>0$, there is a partition $P:t_0=a<t_1<\cdots <b=t_n$ s.t. the sum

$${\Delta }_f(P)=\sum _{j=1}^n(t_j-t_{j-1}){\text{span}}_f([t_{j-1},t_j])<ϵ$$

Notice that ${\Delta }_f(P)$ is the difference between the upper Riemann sum and the lower Riemann sum.

Provided there is a sequence of partitions $P$ s.t. ${\Delta }_f(P)\to 0$, the function is (Riemann) integrable.

Riemann Sum-Based Definition §

Notice that if $P^{\prime }$ is a refinement of $P$, then

$$\begin{array}{rl}L(f,P)& \le L(f,P^{\prime })\\ U(f,P)& \ge U(f,P^{\prime }).\end{array}$$

Define the sets

$$\begin{array}{rl}\mathcal{L}(f)& =\{L(f,P),P\text{ is a partition on }[a,b]\}\\ \mathcal{U}(f)& =\{U(f,P),P\text{ is a partition on }[a,b]\}.\end{array}$$

[!math|{“type”:“lemma”,“number”:“auto”,“setAsNoteMathLink”:false,“_index”:5}] Lemma 6. $\exists \underline{I}=\text{sup }\mathcal{L}(f)$ called the lower integral of $f$. $\exists \overline{I}=\text{inf }\mathcal{U}(f)$ called the upper integral of f called the upper integral of $f$.

\begin{proof} We will show $\mathcal{L}$ is bounded above and $\mathcal{U}$. Suppose $P,P^{\prime }$ are partitions of $[a,b]$. Let $P^{\prime \prime }$ be a common refinement. Then,

$$L(f,P)\le L(f,P^{\prime \prime })\le U(f,P^{\prime \prime })\le U(f,P^{\prime }).$$

Thus, $\mathcal{L}$ is bounded above by $U(f,P^{\prime })$ and $\mathcal{U}$ is bounded below by $L(f,P)$. \end{proof} Note that

$$\underline{I}(f)\le \overline{I}(f).$$

[!math|{“type”:“lemma”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Integrable”,“label”:“integrable”,“_index”:6}] Lemma 7 (Integrable). A bounded function $f$ is integrable over $[a,b]$ iff $\underline{I}(f)=\overline{I}(f)$.

\begin{proof} If $f$ is integrable, then ${\Delta }_f(P)=U(f,P)-L(f,P)$ can be arbitrarily small, so $\underline{I}(f)=\overline{I}(f)$.

Conversely, if $\underline{I}(f)=\overline{I}(f)$, then for any $ϵ>0$, exists $P,P^{\prime }$ s.t. $U(f,P^{\prime })-L(f,P)<ϵ$. Taking a common refinement $P^{\prime \prime }$, we get

$$U(f,P^{\prime \prime })-L(f,P^{\prime \prime })<ϵ,$$

so $f$ is integrable. \end{proof}

When $\underline{I}(f)=\overline{I}(f)$, the integral of $f$ is $I(f)=\underline{I}(f)=\overline{I}(f)$.

Definite Integral §

$${\int }_a^{b}f(x)dx.$$

• definite integral
• b/c definite value
• $f$ is integrand
• $a$ is lower limit
• $b$ is upper limit
• generally

$${\int }_b^{a}f(x)dx=-{\int }_a^{b}f(x)dx.$$

Properties §

[!math|{“type”:“proposition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Sum”,“label”:“sum”,“_index”:7}] Proposition 8 (Sum). If $f,g$ are integrable over $[a,b]$,

$${\int }_a^b(f(x)+g(x))dx={\int }_a^{b}f(x)dx+{\int }_a^{b}g(x)dx$$

\begin{proof} First, note that

$$\begin{array}{rl}{\text{inf}}_{f+g}([c,d])& \ge {\text{inf}}_f([c,d])+{\text{inf}}_g([c,d])\\ {\text{sup}}_{f+g}([c,d])& \le {\text{sup}}_f([c,d])+{\text{sup}}_g([c,d]).\end{array}$$

Then, for any partition $P$,

$$\begin{array}{rl}L(f+g,P)& \ge L(f,P)+L(g,P)\\ U(f+g,P)& \ge U(f,P)+U(g,P)\end{array}$$

Then,

$$\begin{array}{rl}\underline{I}(f+g)& \ge \underline{I}(f)=\underline{I}(g)\\ \overline{I}(f+g)& \le \overline{I}(f)+\overline{I}(g).\end{array}$$

But since $f$ and $g$ are both integrable, $\underline{I}(f)=\overline{I}(f)$ and $\underline{I}(g)=\overline{I}(g)$, so

$$\overline{I}(f+g)\le I(f)+I(g)\le \underline{I}(f+g)$$

which means

$$\underline{I}(f+g)=\overline{I}(f+g)=I(f+g)=I(f)+I(g)$$

\end{proof}

Similarly,

[!math|{“type”:“proposition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Product of Integrable Functions and a Constant”,“label”:“product-of-integrable-functions-and-a-constant”,“_index”:8}] Proposition 9 (Product of Integrable Functions and a Constant). If $f$ is integrable over $[a,b]$, so is $\alpha f$ and

$${\int }_a^b\alpha f(x)dx=\alpha {\int }_a^{b}f(x)dx.$$

[!math|{“type”:“proposition”,“number”:“auto”,“setAsNoteMathLink”:false,“_index”:9}] Proposition 10. If $a,b,c\in \mathbb{R}$ with $a<b<c$, $f$ is integrable on $[a,c]$ iff $f$ is integrable on $[a,b]$ and $[b,c]$, and

$${\int }_a^{c}f(x)dx={\int }_a^{b}f(x)dx+{\int }_b^{c}f(x)dx$$

\begin{proof} Given partitions $P,P^{\prime }$ of $[a,b],[b,c]$, $P\cup P^{\prime }$ is a partition of $[a,c]$. Conversely, if $P^{\prime \prime }$ is a partition of $[a,c]$ we can refine it by adding $b$ and get a partition of the form $P\cup P^{\prime }$. Then, using the sum of upper or lower integrals, we can prove that the integrals are equal. \end{proof}

Techniques §

• integration by substitution
• integration by parts

Integration by Substitution §

Let $g$ be a function that is differentiable on an open interval including $[a,b]$ with $g^{\prime }$ continuous on $[a,b]$. If $f$ is continuous on $[a,b]$, then

$${\int }_a^{b}f(g(x))g^{\prime }(x)dx={\int }_{g(a)}^{g(b)}f(u)du.$$

\begin{proof} Let $\varphi$ be a primitive of $f$ (this exists because continuous functions on closed intervals are always integrable). By Second Fundamental Theorem of Calculus,

$${\int }_{g(a)}^{g(b)}f(u)du=\varphi (g(b))-\varphi (g(a))=\varphi \circ g(b)-\varphi \circ g(a).$$

Chain rule gives

$$(\varphi \circ g{)}^{\prime }(x)={\varphi }^{\prime }(g(x))g^{\prime }(x)=f(g(x))g^{\prime }(x).$$

Applying the Second Fundamental Theorem of Calculus again, we get

$${\int }_a^{b}f(g(x))g^{\prime }(x)dx={\int }_a^b(\varphi \circ g{)}^{\prime }(x)dx=\varphi \circ g(b)-\varphi \circ g(a).$$

\end{proof}

Integration by Parts §

Let $f,g$ be differentiable functions on an open interval containing $[a,b]$ s.t. $f^{\prime },g^{\prime }$ are continuous on $[a,b]$. Then,

$${\int }_a^{b}f(x)g^{\prime }(x)dx=[f(x)g(x){]}_a^b-{\int }_a^b{f}^{\prime }(x)g(x)dx.$$

\begin{proof} By product rule,

$$(fg{)}^{\prime }(x)=f(x)g^{\prime }(x)+f^{\prime }(x)g(x).$$

Rearranging,

$$f(x)g^{\prime }(x)=(fg{)}^{\prime }(x)-f^{\prime }(x)g(x).$$

Integrating and using the second fundemental theorem, we get

$$\begin{array}{rl}{\int }_a^{b}f(x)g^{\prime }(x)dx& ={\int }_a^b(fg{)}^{\prime }(x)dx-{\int }_a^b{f}^{\prime }(x)g(x)dx\\ & =[f(x)g(x){]}_a^b-{\int }_a^b{f}^{\prime }(x)g(x)dx.\end{array}$$

\end{proof}

Polar Coordinates §

If $S$ is an angular sector bounded by $\theta =a,\theta =b$, and $r=e$ with $b-a\in [0,2\pi ]$, then its area is

$$A(s)=\frac{1}{2}(b-a)e^2.$$

We apply the same concept to an area bounded by a radial set bounded by $\theta =a,\theta =b,r=f(\theta )$.

Let $R$ be a radial set bounded by $\theta =a,\theta =b,r=f(\theta )$, where $f^2$ is integrable on$[a,b]$ and $b-a\in [0,2\pi ]$, Then,

$$A(R)=\frac{1}{2}{\int }_a^{b}f(\theta {)}^{2}d\theta .$$

\begin{proof} Fix a partition

$$P:a=t_0<t_1<\cdots <t_n=b.$$

For every integer $j:1\le j\le n$, let

$$\begin{array}{rl}{m}_j& ={\text{inf}}_f([t_{j-1},t_j])\\ M_j& ={\text{sup}}_f([t_{j-1},t_j]).\end{array}$$

Denote $S_j,S_j^{\prime }$ as the angular sectors with radii $m_j,M_j$ between $\theta =t_{j-1}$ and $\theta =t_j$. Then,

$$\frac{1}{2}L(f^2,P)=\frac{1}{2}\sum _{j=1}^n(t_j-t_{j-1})m_j^2=\sum _{j=1}^{n}A(S_j)$$

and, similarly,

$$\frac{1}{2}U(f^2,P)=\sum _{j=1}^{n}A(S_j^{\prime }).$$

Therefore,

$$\frac{1}{2}L(f^2,P)\le A(R)\le \frac{1}{2}U(f^2,P).$$

Since $f^2$ is integrable, $L$ and $U$ converge to a common limit, which is

$$\frac{1}{2}{\int }_a^b{f}^2(x)dx$$

as required. \end{proof}

Improper Integrals §

Let $f$ be a function defined on the interior of an interval $J:[a,b]$ s.t. either $b=\infty$ or $f$ becomes unbounded as $x\to b$. Suppose $a$ is finite and $f(a)$ is defined. Then, ${\int }_{J}f(x)dx$ exists if

1. for every $u\in (a,b)$, $f$ is integrable on $[a,u]$.
2. $\exists$

$$\underset{u\to b,u<b}{\lim }{\int }_a^{u}f(x)dx$$

Then,

$${\int }_a^{b}f(x)dx=\underset{u\to b,u<b}{\lim }{\int }_a^{u}f(x)dx.$$

The same applies for $a$:

$${\int }_a^{b}f(x)dx=\underset{u\to a,u>a}{\lim }{\int }_u^{b}f(x)dx.$$

Both of the above limits are improper integrals.