Finite Automata §

• simple model of Computation
• reads input left to right, one symbol at a time
• maintains state
  • information about seen inputs
  • finite automaton $⟹$ finite # of states (loses memory over time)
• described by diagram or formally

Diagram §

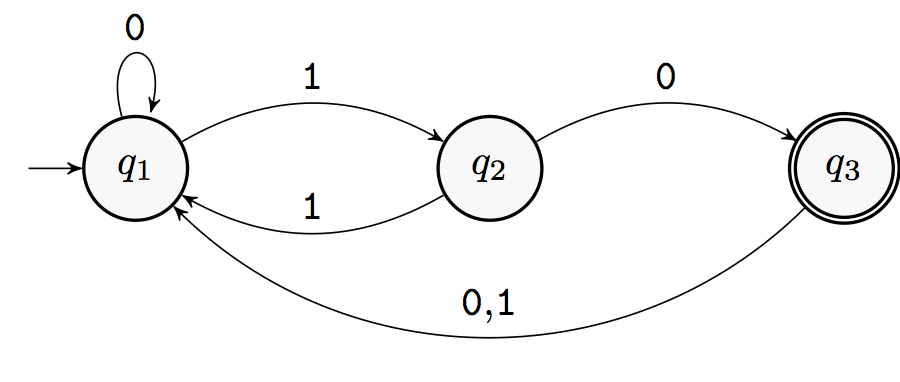
• start arrow at left
• alphabet in example: $\{0,1\}$
• states: $q_1,q_2,q_3$
  • $q_3$ is accept state
• transitions are arrows denoted by number (input)
• this FA decides $L=\{x:x\in \{0,1{\}}^{\ast },x_{n-1}=1\wedge x_n=0\}$
  • language is every string ending with $10$

Formal Definition §

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Finite Automaton”,“label”:“finite-automaton”,“_index”:0}] Definition 1 (Finite Automaton). A finite automaton is a 5-tuple

$$\left(Q,\Sigma ,\sigma ,q_0,F\right)$$

• $Q$: finite set called the states
• $\Sigma$: finite set called the alphabet
• $\delta$: function $Q\times \Sigma \to Q$ called transition function
• $q_0$: start state
• $F$: subset of $Q$ containing accept states

FA Languages §

• closure union ”$C=A\cup B$”
  • set of languages recognized by FA is closed under union
• closure under concatenation ”$C=A\circ B$”
  • $A\circ B=\{xy:x\in A\wedge y\in B\}$
• closure under $\star$
  • $C=A^{\star }=x_1{x}_2\dots ,x_i\in A$

But,

• how to concatenate?
  • can try turning accept states of $A$ into start states of $B$
  • but then FA might start parsing string for $B$ when it should still be parsing $A$
  • need free transition $ϵ$
  • multiple transitions with same label?!
  • introduces non-determinism, creating

Non-Deterministic Finite Automaton §

• can think of NFA operation as
• $x$ is accepted if there exists a way of inserting $ϵ$’s into $x$ so that
• there exists a path of transitions from start to accept state.

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“Nondeterministic Finite Automaton”,“label”:“nondeterministic-finite-automaton”,“_index”:1}] Definition 2 (Nondeterministic Finite Automaton).

$$(Q,\Sigma ,\delta ,q_0,F)$$

• $Q,\Sigma ,q_0,F$ are same as ^02be7c
• $\delta :Q\times (\Sigma \cup \{ϵ\})\to P(Q)$ where $P$ is Power Set of $Q$.

[!math|{“type”:“definition”,“number”:“auto”,“setAsNoteMathLink”:false,“title”:“NFA Operation”,“label”:“nfa-operation”,“_index”:2}] Definition 3 (NFA Operation). NFA $M$ accepts a string $w=w_1{w}_2{w}_3\dots w_n\in {\Sigma }^{\ast }$ if $w$ can be written as

$$y=y_1{y}_2{y}_3\dots y_m\in (\Sigma \cup \{ϵ\}{)}^{\ast }$$

and $\exists$ $r_0,r_1,\dots ,r_m$ of states for which $r_0=q_0$, $r_{i+1}\in \delta (r_i,y_{i+1})$ for $i=0,1,\dots ,m-1$ and $r_m\in F.$

NFA and FA Equivalence §

[!math|{“type”:“theorem”,“number”:“auto”,“setAsNoteMathLink”:false,“_index”:3}] Theorem 4. A language $L$ is recognized by a finite automata iff $L$ is recognized by a non-deterministic finite automata.

\begin{proof} Since FA are NFA, it is trivial to prove recognition by FA $⟹$ recognition by NFA.

To prove NFA recognition $⟹$ FA recognition, we prove all NFA can be simulated by FA - by setting states of FA to be subsets of the set of states of NFA. That is, given NFA $M=(Q,\Sigma ,\delta ,q_0,F)$, we can construct simulation FA $M^{\prime }=(Q^{\prime },{\Sigma }^{\prime },{\delta }^{\prime },q_0^{\prime },F^{\prime })$ where

• $Q^{\prime }=P(Q)$,
• $F^{\prime }=\{R\in Q^{\prime }:Q\text{ contains accept state of }M\}$
• ${\delta }^{\prime }$: ${\delta }^{\prime }(R,a)={\cup }_{r\in R}E(\delta (r,a))$
  • $E=$
• $q_0^{\prime }=$

Now we should prove construction works by induction on number of steps of computation but nah. \end{proof}

Limitations §

We can prove that there are languages FA can’t recognize through the existence of Non Regular Languages.