Line Integrals

Derivation for 3D Surface Area §

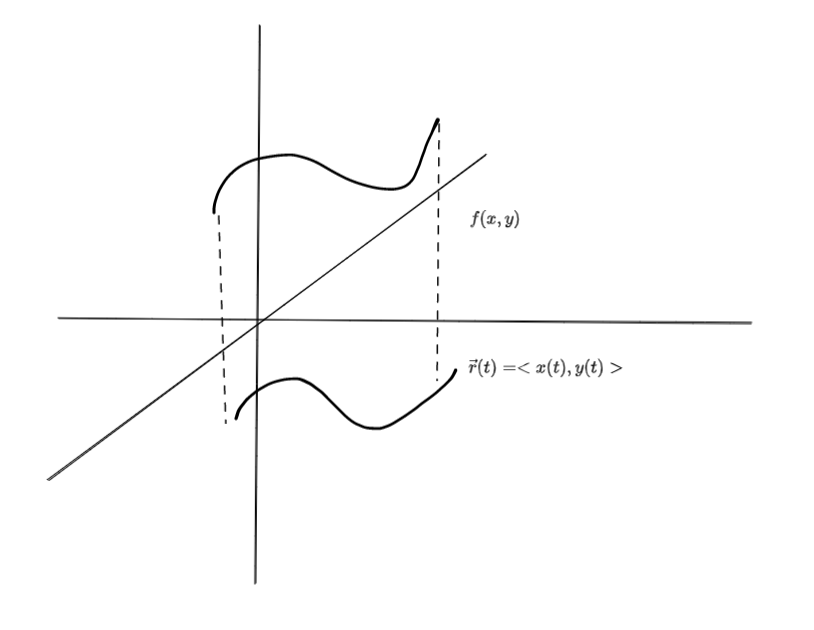
The formula for the surface area is

$$A={\int }_a^{b}f(x,y)dS$$

We know that

$$\begin{array}{rl}dS& =\sqrt{(dx{)}^2+(dy{)}^2}\\ & =\frac{1}{dt}\sqrt{(dx{)}^2+(dy{)}^2}dt\\ & =\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}dt\end{array}$$

So the final surface area formula becomes

$$\begin{array}{rl}A& ={\int }_a^{b}f(x,y)\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}dt\\ & ={\int }_a^{b}f(x(t),y(t))\mid \mid r(t)\mid \mid dt\end{array}$$

Uses §

• calculate area of curvy sheet with given height
• measure mass of wire
• work done of particle moving in the force field

Examples §

Example 1 §

Evaluate the line intergal ${\int }_C\frac{x+y+z}{5}ds$ and C is the curve $\vec{r}(t)=<4t,8\cos \frac{3}{8}t,8\sin \frac{3}{8}t,0\le t\le \frac{8\pi }{3}$

$$\begin{array}{rl}{r}^{\prime }(t)& =<4,-3\sin \frac{3}{8}t,3\cos \frac{3}{8}t>\\ \mid \mid r^{\prime }(t)\mid \mid & =5\\ I& ={\int }_0^{\frac{8\pi }{3}}+\frac{4t+8\cos \frac{3}{8}t+8\sin \frac{3}{8}t}{5}5dt=183.03\end{array}$$

Example 2 §

Find mass of wire that lies along the curve $\vec{r}(t)=(\frac{\sqrt{7}}{2}{t}^2-4)\hat{i}+3t\hat{j},0\le t\le 1,\rho =4t$

$$\begin{array}{rl}{r}^{\prime }(t)& =<\sqrt{t},3>\\ ||r^{\prime }(t)||& =\sqrt{7t^2+9}\\ M& ={\int }_0^{1}4t\sqrt{7t^2+9}dt=7.05\end{array}$$

Example 3 §

Evaluate ${\int }_C(y+z)ds$ where $C=(0,0,0)\to (4,4,1)$ given $C_1:r(t)=4t^2\hat{i}+4t\hat{j},0\le t\le 1$ and $C_2:r(t)=4\hat{i}+4\hat{j}+(t-1)\hat{k}$

Path 1 §

$$\begin{array}{rl}{r}^{\prime }(t)& =<8t,4>\\ S& ={\int }_0^{1}4t\sqrt{64t^2+16}dt\\ & =\end{array}$$

Path 2 §

$$\begin{array}{rl}{r}^{\prime }(t)& =<0,0,1>⟹||r^{\prime }(t)||=1\\ S& ={\int }_1^2(3+t)1dt\\ & =\end{array}$$

Line Integral with Vector Field §

Uses §

For $\vec{F}(x,y,z)$ represent a force field on on particle and $\vec{r}(t)=<x(t),y(t),z(t)>$ at $a\le t\le b$.

The work done is

$$\begin{array}{rl}W& ={\int }_C\vec{F}\cdot \vec{T}dr\\ & ={\int }_C\vec{F}\frac{{\vec{r}}^{\prime }(t)}{\mid {\vec{r}}^{\prime }(t)\mid }|{\vec{r}}^{\prime }(t)|dt\\ & ={\int }_C\vec{F}dr\end{array}$$

Examples §

Example 4 §

Find the work done by $\vec{F}$ over the curve in the direction of increasing $t$.

$$\vec{F}=-8z\hat{i}+8x\hat{j}+3y\hat{k},0\le t\le 1,\vec{r}(t)=<t,t,t>$$

Solution:

$$\begin{array}{rl}{\vec{r}}^{\prime }(t)& =<1,1,1>\\ \vec{F}(t)& =<-8t,8t,3t>\\ W& ={\int }_0^1(-8t+8t+3t)\cdot 1dt\\ & =\frac{3}{2}\end{array}$$

Example 5 §

Find the line integral of ${\int }_{C}2xyds$ where $C$ is the segment $(-2,1)$ to $(1,3)$

Solution:

Setting arbitrary values for $t$, @ $t=0$ C is @ $(-2,1)$, @ $t=1$ C @ $(1,3)$

Using equation of lines:

$$\begin{array}{rl}x& =a_{1}t-2⟹a_1=3\\ y& =a_{2}t+1⟹a_2=2\\ \vec{r}(t)& =<3t-2,2t+1>\\ S& ={\int }_0^{1}2(3t-2)(2t+1)\cdot \sqrt{13}dt\\ & =-\sqrt{13}\end{array}$$

Example 6 §

Find the line intergral $\int x^{2}ds$ where C is the curve.

Solution:

let $x=t$

$$\begin{array}{r}\vec{r}(t)=<t,t^2+1>\end{array}$$