Atoms are made up of electrons (), protons (), and neutrons ().
Electrons are ~ kg. Protons are kg. Neutrons are .
Protons are made from 2 up quarks and 1 down quark. Neutrons are made from 2 down quarks and 1 up quarks. Down quarks are kg, up quarks are kg.
| Particle | Symbol | Mass | Composition | Charge | Mobility |
|---|---|---|---|---|---|
| Proton | 2 up quarks, 1 down quark | + | yes | ||
| Electron | kg | - | |||
| Neutrons | e | 2 down quarks, 1 up quark | 0 | ||
| down quark | d | ||||
| up quark | u |
Millikan Oil Experiment
Purpose of research was to find charge. He tried different kinds of liquids and ended up on vacuum pumped oil because it was perfectly spherical so he can simplify his formula.
To conduct experiment, he shot an extremely small drop of oil and shot an xray to ionize it. It then would pass through an electric field.
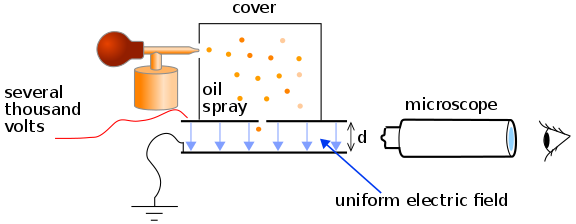
The plan was to equate the force of the electric field on the ionized particle and the gravitational force in
However, finding mass was not easy because
didn’t hold true due to the radius of the spherical drop of oil not being constant.
To solve for mass, he used Stoke’s law, which stated the drag force of the oil drop was
6\pi \eta rv $$and that the force of gravity was(\rho_{0} - \rho_{a})\frac{4}{3}\pi r^{3}g
\begin{align} 6\pi \eta rv &= (\rho_0 - \rho_{a}) \frac{4}{3}\pi r^{3}g \ r &= \sqrt{ \frac{9\eta v}{2g(\rho_{0} - \rho_{a})} } \ \frac{qV}{d} &= \rho_{oil} \frac{4}{3}\pi \left(\sqrt{ \frac{9\eta v}{2g(\rho_{0} - \rho_{a})} }\right)^{3}g \ \implies q &= \frac{\rho_{oil} \frac{4}{3}\pi \left(\sqrt{ \frac{9\eta v}{2g(\rho_{0} - \rho_{a})} }\right)^{3}gd}{V} \ \implies q &= 1.6 \cdot 10^{-19} \text{ Coloumbs} \end{align}
# Coloumb's Law Given two charges $q_{1}$ and $q_{2}$ separated by a distance $r$, the Coloumbic force between them is\vec{F}{e} = \frac{q{1}q_{2}}{r^{2}}
## Neglecting Gravitational Forces at Atomic Level At the atomic level, we can neglect gravitational forces because the Coloumbic forces are so much stronger.\begin{align} \vec{F}{e} &= \frac{(9\cdot 10^{9})(1.6 \cdot 10^{-19}) (1.6\cdot 10^{-19})}{(5\cdot 10^{-10})^{2}} \ \vec{F}{g} &= \frac{(6.67\cdot 10^{-11})(1.6 \cdot 10^{-27}) (9\cdot 10^{-31})}{(5\cdot 10^{-10})^{2}} \ \implies \frac{\vec{F}_{e}}{\vec{F}g} &= 10^{39} \end{align}
# [[Electric Field]], Electric Potential, Work-Energy | Vector | Scalar | | ------------- | ------------- | | $\vec{F} = \frac{kq^{2}}{r^{2}}$ | $U_{e} = \int \vec{F} \, d\vec{r} = \frac{kq^{2}}{r}$ | | $\vec{E} = \frac{kq}{r^{2}}$ | $V = \int \vec{E} \, d\vec{r} = \frac{kq}{r}$ As seen in the table above, electric potential can be describe with an analogy of gravitational potential. It's the g constant.