Electric Field

The electric field of a particle with charge $Q$ is

$$\vec{E}=\frac{kQ}{r^2}$$

because

$${\vec{F}}_e=\frac{kqQ}{r^2}=q\vec{E}⟹\vec{E}=\frac{kQ}{r^2}$$

Visualization §

Given a positive source and a negative sink, we can visualize the electric field as follows:

Electric Flux §

Given an electric field around a particle with charge $Q$, the electric flux is calculated with the formula

$${\varphi }_{electric}=\frac{Q}{{ϵ}_0}=\vec{E}dA,$$

where ${ϵ}_0$ is the permittivity of the space around the particle (how well space stores electrical energy), $A$ is the surface area. This formula is Gauss’s Law.

Since the magnetic field is a sphere,

$$\begin{array}{rl}dA& =R^2{\int }_0^{\pi }\sin \theta d\theta {\int }_0^{2\pi }\varphi d\varphi \\ & =4\pi R^2\\ \vec{E}dA& =\vec{E}\cdot 4\pi R^2\\ ⟹\vec{E}\cdot 4\pi R^2& =\frac{Q}{{ϵ}_0}\\ ⟹\vec{E}& =\frac{kQ}{r^2},\end{array}$$

deriving $k$ to be $\frac{4\pi }{{ϵ}_0}$.

Kinematics/Dynamics §

Velocity §

We can apply kinematics to a charged particle in an electric field to find its velocity.

$$\begin{array}{rl}F=ma& =qE⟹a=\frac{qE}{m}\\ v_f^2& =v_i^2+2ad,v_i=0\\ v_f& =\sqrt{\frac{2qEd}{m}}\end{array}$$

Path of Charged Particles in Field §

Diagram:

Kinematics:

Dipoles §

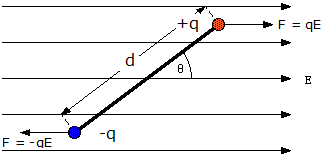
In the above diagram, the charged particles create a torque in the electric field.

$$\begin{array}{rl}\tau & =\frac{d}{2}qE+\frac{d}{2}qE\\ & =qEd\sin \theta \end{array}$$

Solving Field for Different Shapes §

Rod §

Since the y components of the electric field cancel out due to vertical symmetry, we only need to solve for

$$\begin{array}{rl}E& =\int d{E}_x\\ & =\int \frac{k}{r^2}\cos \theta dq\end{array}$$

Given that

$$\begin{array}{rl}r& =\sqrt{x^2+y^2}\\ \cos \theta & =\frac{x}{r}=\frac{x}{\sqrt{x^2+y^2}}\\ \lambda =\frac{Q}{L}=\frac{dq}{dy}⟹dq& =\frac{Q}{L}dy\end{array}$$

We can rewrite our integral for the electric field as

$$\begin{array}{rl}E& =\int \frac{k}{(\sqrt{x^2+y^2}{)}^2}\cdot \frac{x}{\sqrt{x^2+y^2}}\cdot \frac{Q}{L}dy\\ & =\frac{kQx}{L}{\int }_{-\frac{L}{2}}^{\frac{L}{2}}\frac{dy}{(x^2+y^2{)}^{\frac{3}{2}}}\\ & =\frac{kQ}{x\sqrt{x^2+\frac{L^2}{4}}}\end{array}$$

We can verify that this answer works by taking the limit of the expression as $L\to 0$.

$$\underset{L\to 0}{\lim }\vec{E}=\frac{kQ}{x^2}$$

This makes sense because as the length of a rod approaches 0, it is simply a point, and we have rederived the expression for the electric field of a point charge.

Electric Field Within Shapes §

To solve for electric fields within shapes, we must use Gauss’s Law.