Quantum Mechanics

1. energy is quantized
2. particles display wave-like behavior

Energy Quantization §

• evident through black-body radiation experiment by Plancke
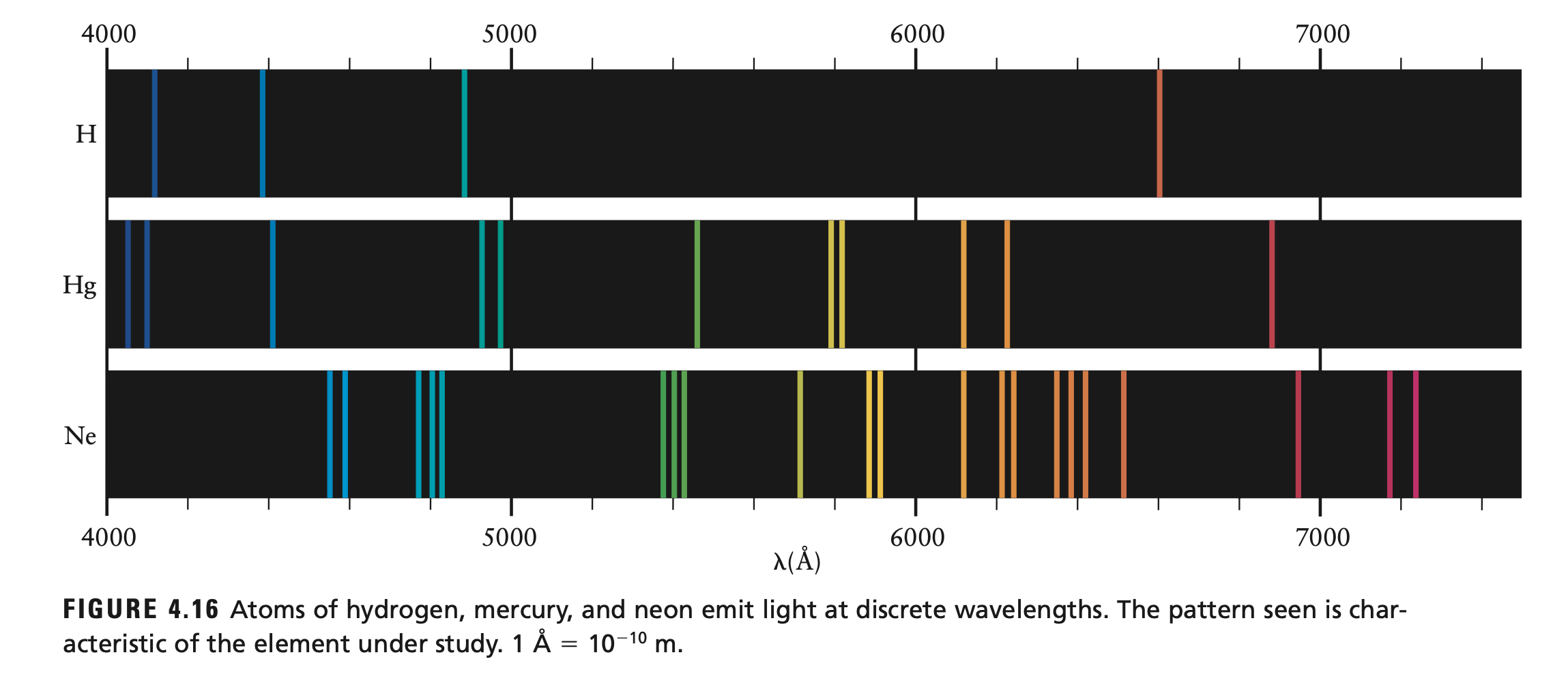
• evident through atomic emission spectrum

• Franck-Hertz experiment showed the atoms have energy levels because electrons colliding with gaseous atoms only gain energy when they have a certain energy at a threshold voltage

Bohr Model §

• connects continuous energy to quantized energy of electron seen above
• model of hydrogen atom with discrete energy states
• frequency of light absorbed is related to change in energy state

$$\Delta E=hv⟺v=\frac{E_f-E_i}{h}$$

• based on Rutherford’s model: electron orbits around nucleus

$$E=KE+PE=\frac{1}{2}{m}_e{v}^2-\frac{Z{e}^2}{4\pi {ϵ}_{0}r}$$

• $Z$ is effective nuclear charge
• can relate force to magnitude of force with velocity using centripetal motion

$$\begin{array}{c}|F_{\text{Couloumb}}|=|m_e\vec{a}|\\ \frac{Z{e}^2}{4\pi {ϵ}_0{r}^2}=m_e\frac{v^2}{r}\end{array}$$

• impossible in classical physics
  • electron is accelerating implies emits EM radiation
  • should eventually collide with nucleus
• Bohr avoids above conflict by assuming electron can only occupy discrete orbits
  • characterized by radius $r_n$, energy $E_n$
• angular momentum is also quantized in multiples of $\frac{h}{2\pi }$, $h$ is Plancke’s constant

$$L=m_{e}vr=n\frac{h}{2\pi },n=1,2,3,\dots$$

• can solve for $v$, plug into force equation, get $r$

$$\begin{array}{c}v=\frac{nh}{2\pi m_{e}r}\\ r_n=\frac{{ϵ}_0{n}^2{h}^2}{\pi Z{e}^2{m}_e}=\frac{n^2}{Z}{a}_0\end{array}$$

• $a_0=5.29\cdot 10^{-11}\text{ m}$ is Bohr’s radius, allows us to get clean formula
• can substitute $r$ and $v$ to get $E$

$$E_n=-\frac{Z^2{e}^4{m}_e}{8{ϵ}_0^2{n}^2{h}^2}=-(2.18\cdot 10^{-18}\text{ J})\frac{Z^2}{n^2},n=1,2,3,\dots$$

• expressed in energy unit rydberg

Ionization Energy §

• consistent with IE of hydrogen atom
  • ionization is equivalent to Bohr model transition from $n=1\to n=\infty$

$$\Delta E=E_f-E_i=0-(-2.18\cdot 10^{-18}\text{ J})=2.18\cdot 10^{-18}\text{ J}$$

• multiply above value by Avogadro’s number to get $\frac{kJ}{mol}$ yields the correct value for IE

Atomic Spectra §

• can also be used to explain colors in atomic spectra

$$hv=\Delta E=\frac{Z^2{e}^4{m}_e}{8{ϵ}_0^2{h}^2}\left[\frac{1}{n_f^2}-\frac{1}{n_i^2}\right]$$

• since $n_f,n_i\in \mathbb{N}$, we get lines of light of certain colors (frequencies)

Wave-Particle Duality §

• Bohr’s model modeled energy quantization but didn’t explain origin
• need concept of wave-particle duality
  • particles can behave like waves and vice versa

Photoelectric Effect §

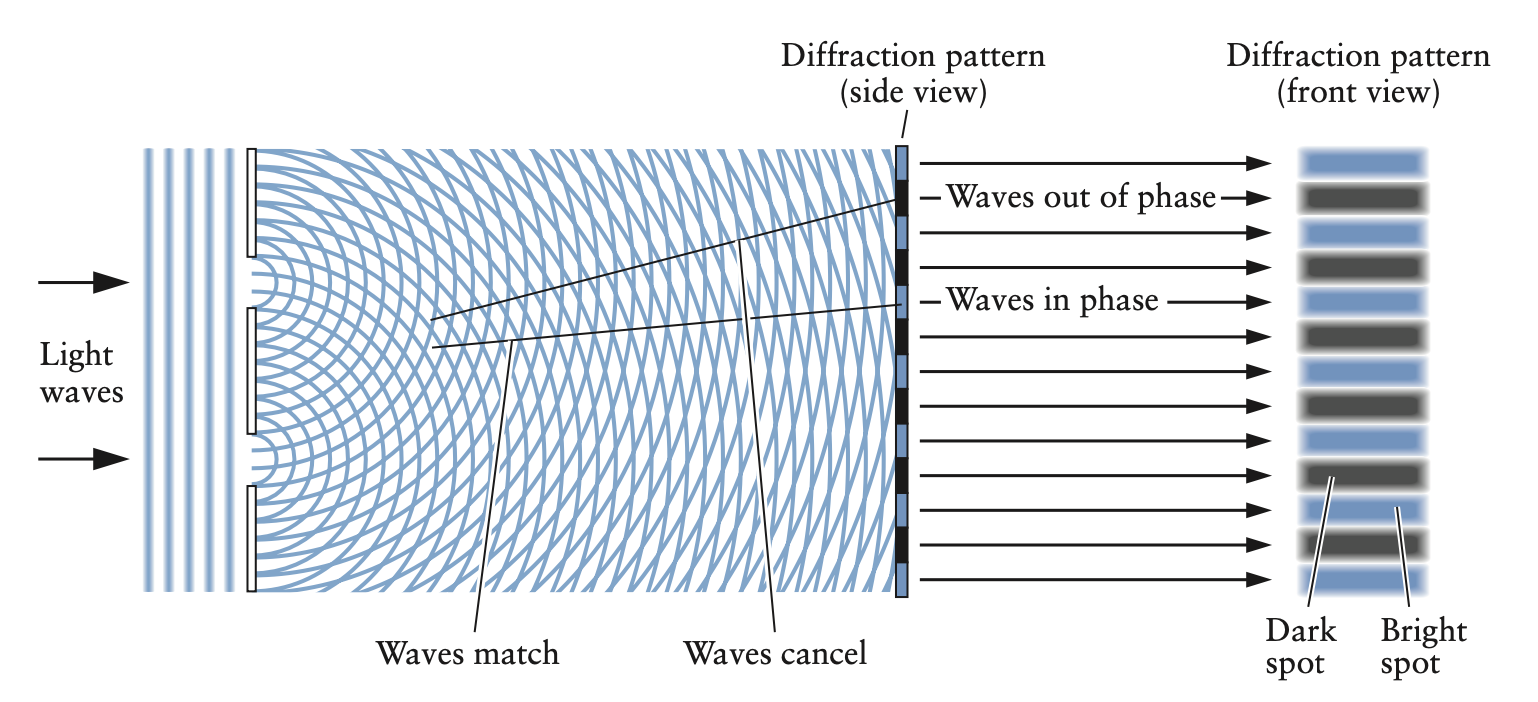
• light behaves like waves through constructive and destructive interference in experiments

• light waves also behave like particles (photons)

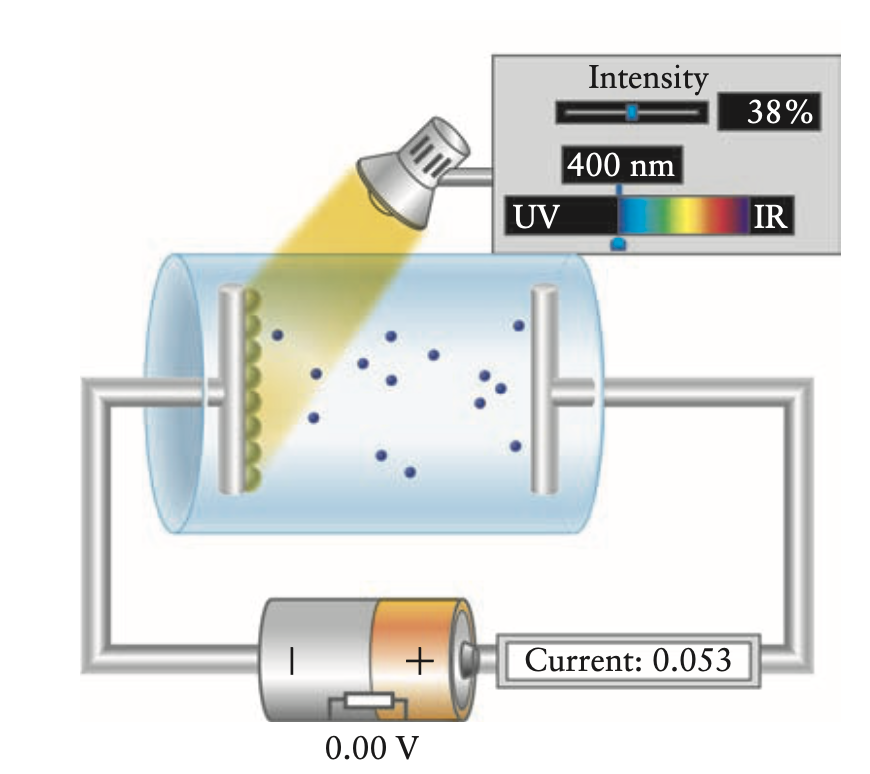
• light shining on surface of metal can eject electrons (photoelectrons) and create current
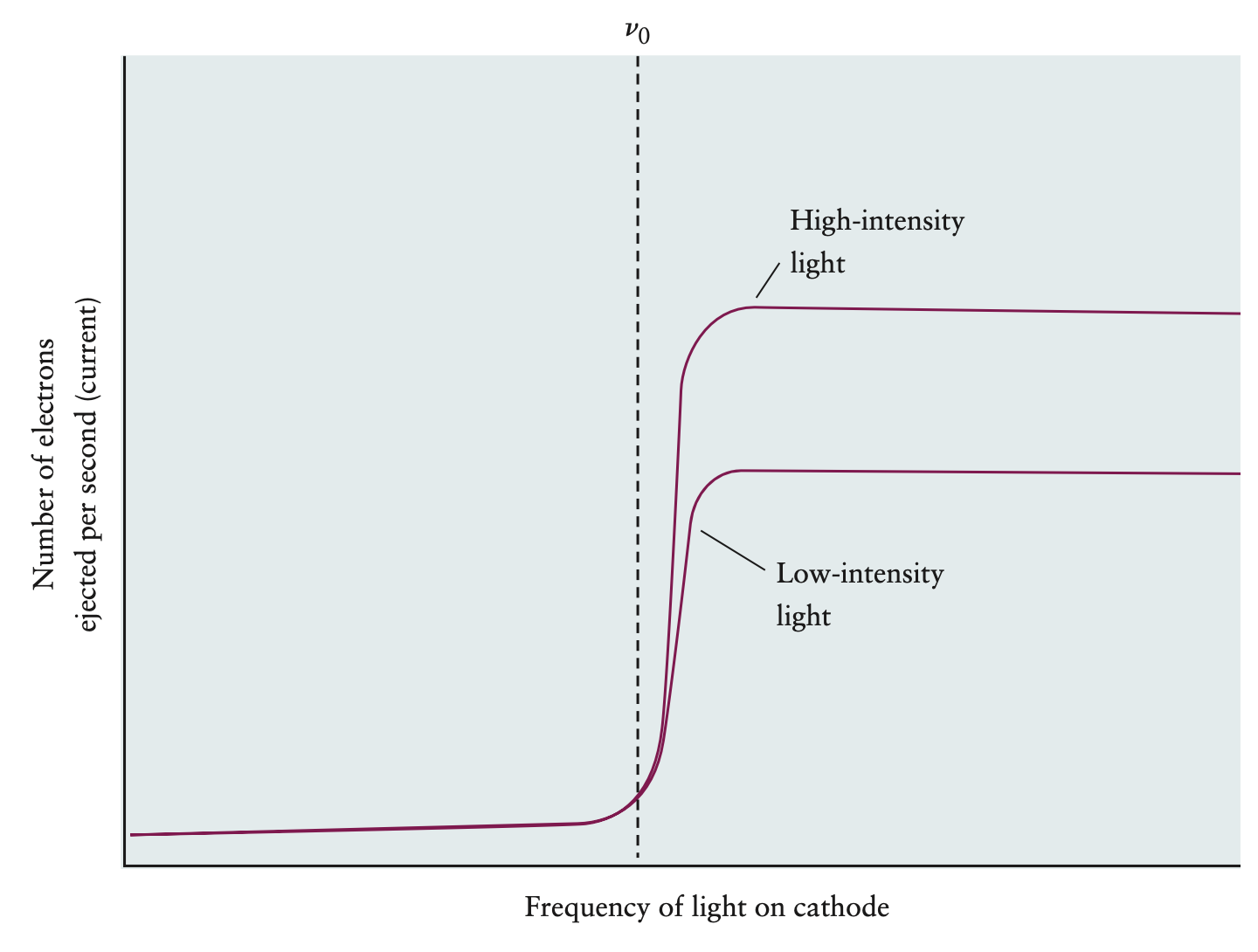
• electrons are only ejected after a certain threshold frequency of light
  • intensity doesn’t cut it
  • figure below relates intensity, frequency, current

• voltage applied by battery in experiment diagram can be used to measure the energy required by the light
  • electron has less maximum kinetic energy energy $E_{max}$ than $eV$ means it won’t make it across voltage, thus no current
• concept of photon explains connection between threshold frequency $v_0$ and max kinetic energy $E_{max}$
  • photon is quanta of energy of light, like a particle
  • $E_{\text{photon}}=hv$
  • metal absorbs photon, photoelectron gains energy to escape nucleus
  • photoelectron loses energy $E^{\prime }$ from collisions with other atoms and $\Phi$ in escaping the surface
  • conservation of energy:

$$hv=E^{\prime }+\Phi +E_{\text{kin}}$$

• electrons with $E_{max}$ come from surface, where $E^{\prime }=0$
• thus,

$$E_{\text{max}}=\frac{1}{2}m{v}_e^2=hv-\Phi$$

• $\Phi =h{v}_0$ is a constant characteristic of metal
• key point of Einstein’s photon is that photon does all or nothing

De Broglie Waves §

• EM radiation behaves like traveling waves
  • $A$: amplitude
  • $\lambda$: wavelength
  • $\nu$: frequency

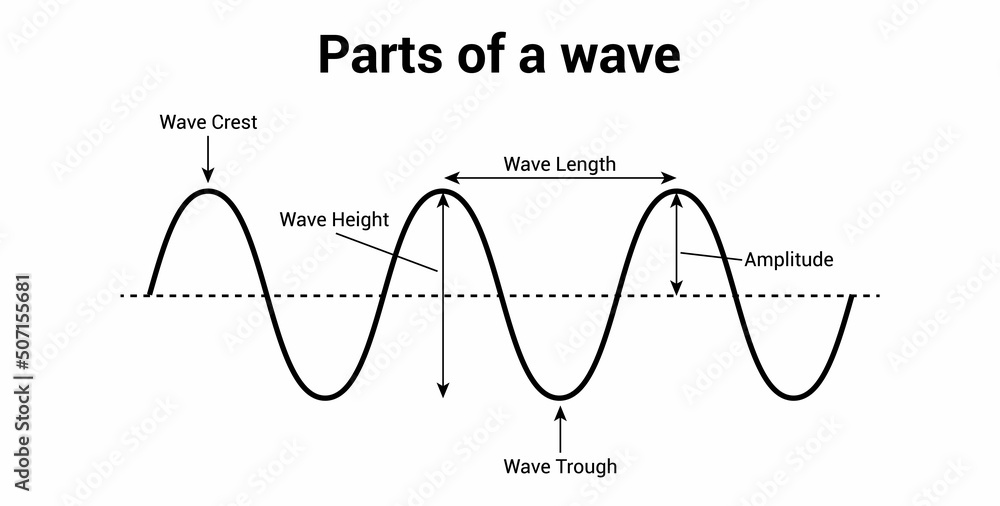
• there are also standing waves
  • example: guitar string is fixed at both ends (boundary conditions), thus only certain oscillations are possible
  • condition for allowed wavelengths is

$$n\frac{\lambda }{2}=L,n=1,2,3\dots$$

• every value of $n$ corresponds to a harmonic
• higher harmonic has more nodes, aka points in wave where $A=0$
• De Broglie standing waves perfectly describe quantization
  • quantum number $n$ relates to harmonics
  • electrons behave like circular standing waves
    • $n\lambda =2\pi r$

• matches the relationship for angular momentum described by Bohr

$$m_{e}vr=n\frac{h}{2\pi }⟺2\pi r=n\left[\frac{h}{m_{e}v}\right]$$

• De Broglie used theory of relativity to extend this to photons too
  • generalization: any particle moving with linear momentum $p$ has wavelike properties and $\lambda =\frac{h}{p}$
• De Broglie waves imply Heisenberg Uncertainty Principle
  • cannot know position of momentum at any one time
• wave-like properties imply electrons can be modeled by wave function, which led to

Schrodinger’s Equation §

$$\hat{H}\Psi =E\Psi$$

• $\Psi$ is the electronic wavefunction
  • depends on $(x,y,z,t)$, aka position of electron and time

Origin §

Consider a particle moving freely along the x-axis with momentum $p$. It must have wavelength $\lambda =\frac{h}{p}$. Two wave functions that work are

$$\begin{array}{rl}\psi (x)& =A\sin \frac{2\pi x}{\lambda }\\ \psi (x)& =B\cos \frac{2\pi x}{\lambda }.\end{array}$$

The second derivative of either function is

$$\frac{d^2\psi (x)}{d{x}^2}=-A{\left(\frac{2\pi }{\lambda }\right)}^2\psi (x).$$

Replacing $\lambda$ with $\frac{h}{p}$ from de Broglie’s relation, we get

$$-\frac{h^2}{8{\pi }^{2}m}\frac{d^2\psi (x)}{d{x}^2}=\frac{p^2}{2m}\psi (x)=K\psi (x)$$

where $K=\frac{p^2}{2m}$ is the kinetic energy of the particle. Including external forces from the walls around the particle or the presence of fixed charges and using $E$ to represent the total energy, we get

$$-\frac{h^2}{8{\pi }^{2}m}\frac{d^2\psi (x)}{d{x}^2}+V(x)\psi (x)=E\psi (x).$$

Letting the Hamiltonian operator $\hat{H}$ denote the energy of the wave function, we get

$$\hat{H}\Psi =E\Psi .$$

Interpreting Energy §

• potential $V(x,y,z)$ doesn’t vary with time $⟹$
• Schrodinger’s equation can only be solved for specific values of $E$
• thus, Schrodinger’s equation $⟹$ energy quantization
• time independent wave function state = stationary state
  • every stationary state has different energies and different wave functions
  • lowest energy = ground state, other energy = excited state

Interpreting Wave Function §

The classical electromagnetism view of light states

$$\text{intensity}\propto (E_{max}{)}^2.$$

If light is photons, the intensity is the probability of finding a photon. This analogy $⟹$ ${\psi }^2$ is the probability density of a particle is the probability density function:

$$|\psi (x,y,z){|}^{2}dV$$

is the probability that a particle will be found in a region of volume $dV$ centered at $(x,y,z)$.

Probability density is normalized since sum of all probabilities is 1:

$${\int }_{-\infty }^{\infty }|\psi (x){|}^{2}dx=1.$$

Normalization also implies that

1. $\psi ,{\psi }^{\prime }$ are continuous
2. $\psi$ is bounded, or as $x\to \pm \infty$, $\psi \to 0$.

Solving the Equation §

• can simulate solving the equation with a Particle in a Box Model simulation
  • not complete solution, only for one electron system
• solution for energy demonstrates energy quantization
• can’t actually solve equation for real case scenarios

Relationship to Atomic Orbitals §

• solution of Schrodinger’s Equation for one-electron atom when replacing potential energy with Coulomb potential quantizes 3 values, known as quantum numbers

Molecular Orbitals §

• Quantum mechanics can be used to explain Molecular Orbitals