Lorentz Transformation

To transform events between reference frames, we use the Lorentz Transformation.

The Need for a Better Transformation §

• imagine the two reference frames below

• according to Galilean Transformation

$$\begin{array}{rl}{x}^{\prime }& =x-Vt\\ y^{\prime }& =y\\ z^{\prime }& =z\\ t^{\prime }& =t\end{array}$$

• this transform is flawed
• length and time are frame-independent (can’t be true as seen in Intro to Special Relativity)
• velocity transformation is $v_x^{\prime }=v_x-V⟹$ light speed is different in different frames (also not true)
• need a robust transformation compatible with length contraction, time dilation, and velocity

Lorentz Transformation §

• sync clocks in both frames to $0$ when origins coincide
• then event occurs at
  • $(x,y,z,t)$ in $S$
  • $(x^{\prime },y^{\prime },z^{\prime },t)$ in $S^{\prime }$

Coordinate Transformation §

• $x$ in terms of $x^{\prime }$:
  • origins are offset by $Vt$
  • observer in $S$ sees $x^{\prime }$ contracted by $\sqrt{1-V^2/c^2}$
  • that means

$$\begin{array}{rl}x& =Vt+x^{\prime }\sqrt{1-V^2/c^2}\\ x^{\prime }& =\frac{x-Vt}{\sqrt{1-V^2/c^2}}\end{array}$$

• since no velocity in $y,z$ directions, $y^{\prime }=y,z^{\prime }=z$

Time Transformation §

• to get new time transformation ($t^{\prime }=T(t)$), we will
  • set up a clock $A$ at rest at $(x,y,z)$ in $S$ frame
  • and observe it from $S^{\prime }$.
  • also place two clocks at origins of $S$ and $S^{\prime }$ that are synced to $0$ when origins coincide
  • clock at origin of $S$ lags clock $A$ by $Vx/c^2$ according to simultaneity
• diagram shown below

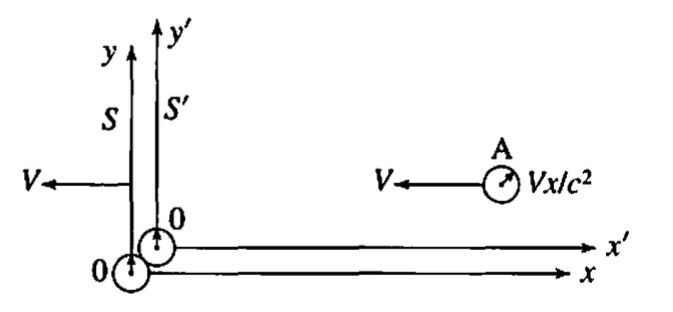
• after $t^{\prime }$ passes in $S^{\prime }$,

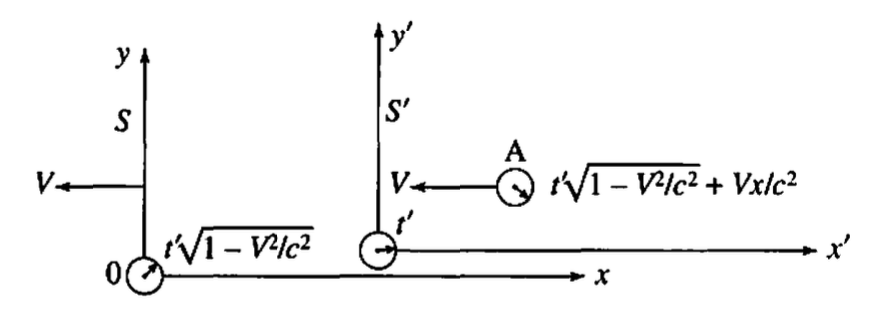
• $S$ has moved to the left
• clock at origin of $S$ runs slow because of time dilation, so reads $t=t^{\prime }\sqrt{1-V^2/c^2}$
• same for clock $A$, plus leading clock lag, so clock $A$ reads $t=t^{\prime }\sqrt{1-V^2/c^2}+Vx/c^2$
• solving for $t^{\prime }$,

$$t^{\prime }=\frac{t-Vx/c^2}{\sqrt{1-V^2/c^2}}$$

Summary §

• substituting $V=\beta c$ (helps with calculations) and
• $\frac{1}{{\gamma }^2}+{\beta }^2=1$ by definition in Significance
• we get

$$\{\begin{array}{l}{x}^{\prime }=\gamma (x-Vt)\\ t^{\prime }=\gamma \left(t-\frac{Vx}{c^2}\right)\end{array}⟺\{\begin{array}{l}{x}^{\prime }=\gamma (x-\beta ct)\\ c{t}^{\prime }=\gamma \left(ct-\beta x\right)\end{array}$$

Notice this is just a linear transformation:

\begin{pmatrix} x' \\ ct' \end{pmatrix} = \begin{pmatrix} \gamma & - \beta\gamma \\ -\beta\gamma & \gamma \end{pmatrix}\begin{pmatrix} x \\ ct \end{pmatrix} .$$ ## Verifying Time Dilation, Length Contraction, and Simultaneity - observe a person moving at $v=\beta c$ for a time $t$ - applying the transformation to get their time:

\begin{align} ct’&=\gamma ct-\beta\gamma x \ &= \gamma ct-\beta\gamma(\beta ct) \ &= \gamma(1-\beta^{2})ct \ \implies t’ &= \frac{t}{\gamma}. \end{align}

- now if the person is horizontal with head at $x_{1}'$ and feet at $x_{2}'$ in their frame and - in our frame, we observe their head at $x_{1}$ and feet at $x_{2}$ when synchronized clocks at $x_{1}$ and $x_{2}$ read $t$, - the length of the person in their rest frame is

D = x_{1}’ - x_{2}’ = \gamma(x_{1}-Vt) - \gamma(x_{2}-Vt) = \gamma(x_{1}-x_{2})

$$-andinourframe,thelengthis$$

x_{1} - x_{2} = \frac{D}{\gamma}

- we can verify simultaneity holds by checking if leading clock lags in both frames - put clock at person's head ($x_{1}'$) and feet ($x_{2}'$) in their rest frame (prime frame) - then, the lag between the two clocks is

t_{1}‘-t_{2}’

$$-applyLorentztransformationtogetintermsofvariablesinourframe$$

t_{1}‘-t_{2}’ = \frac{(t_{1}-t_{2}) - (V / c^{2})(x_{1}-x_{2})}{\sqrt{ 1-V^{2} / c^{2} }}

- if measurement in our frame is simultaneous ($t_{1}=t_{2}$), then

t_{1}‘-t_{2}’ = - \left( \frac{V}{c^{2}} \right) \frac{x_{1}-x_{2}}{\sqrt{ 1-V^{2} / c^{2} }} = -\frac{V}{c^{2}}(x_{1}‘-x_{2}’) = -\frac{V}{c^{2}}D

## Velocity Transformation - now observe the same person, but we move at velocity $V$ - calculating the velocity of the object in our new frame,

\begin{align} \frac{dx’}{dt’}&=\frac{dx’}{dt}\left( \frac{dt}{dt’} \right) \ &= \frac{dx’ / dt}{dt’ / dt} \ \end{align}

- plugging in $x' = \gamma(x-Vt)$, $t' = \gamma(t- \frac{Vx}{c^{2}})$, we get

\begin{align} \frac{dx’}{dt} &= \gamma\left( \frac{dx}{dt}-V \right) \ \frac{dt’}{dt} &= \gamma\left( 1-\left( \frac{V}{c^{2}} \right) \frac{dx}{dt}\right) \ \frac{dx’}{dt’} &= \frac{\gamma(dx / dt - V)}{\gamma(1-(V / c^{2})dx / dt)} \ v_{x}’ &= \frac{v_{x}-V}{1-Vv_{x}/ c^{2}} \end{align}

- for other dimension $y,z$ - person still only moves in $x$

\begin{align} \frac{dy’}{dt’} &=\frac{dy’ / dt}{dt’ / dt} \ &= \frac{dy / dt}{\gamma(1-(V / c^{2})dx / dt)} \ v’{y} &= \frac{v{y}\sqrt{ 1-V^{2} / c^{2} }}{1-Vv_{x} / c^{2}} \end{align}

### Faster than the Speed of Light? - now imagine two spaceships moving towards each other at $0.99c$ and $-0.99c$ - velocity greater than $c$?! - no lol - if we (static observer of event) boost to $0.99c$ - $V=0.99c$ - $v_{x}=-0.99c$

\begin{align} v_{x}’ &= \frac{-0.99c - 0.99c}{1-\frac{(0.99)(-0.99)c^{2}}{c^{2}}} \ &= -\frac{1.98c}{1.9801} \ &= -0.99995c \end{align}