RC Circuits

Summary of: https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Book%3A_University_Physics_II_-_Thermodynamics_Electricity_and_Magnetism_(OpenStax)/10%3A_Direct-Current_Circuits/10.06%3A_RC_Circuits

RC circuits are circuits with a resistor and a capacitor.

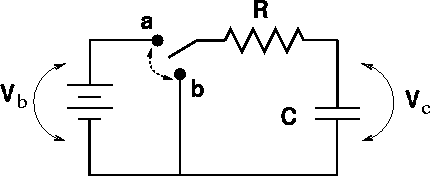
Charging §

When battery and capacitor are connected, capacitor charges until

$$ϵ=V_B=V_C$$

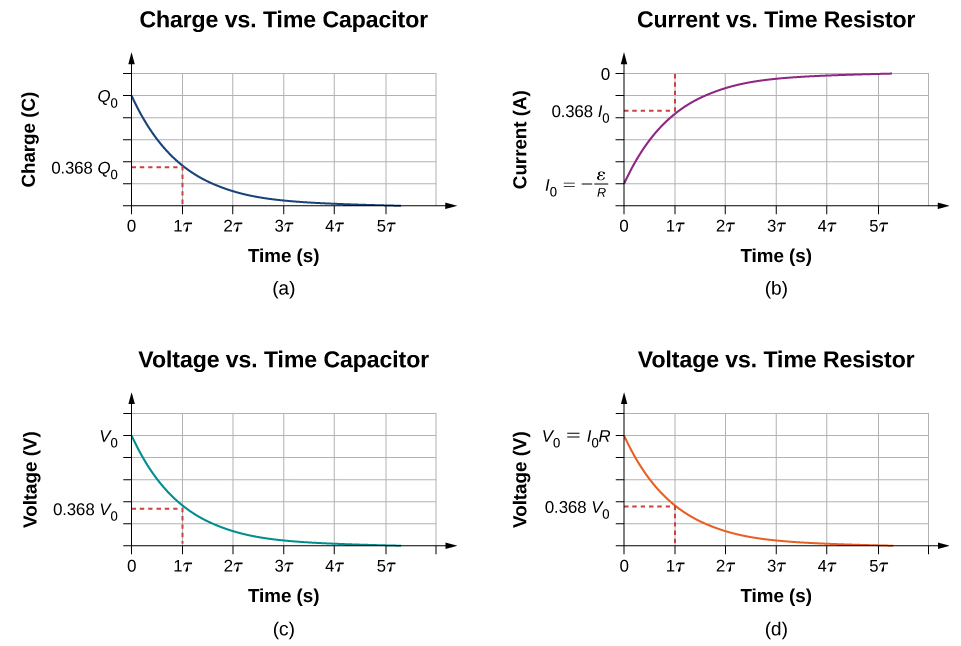
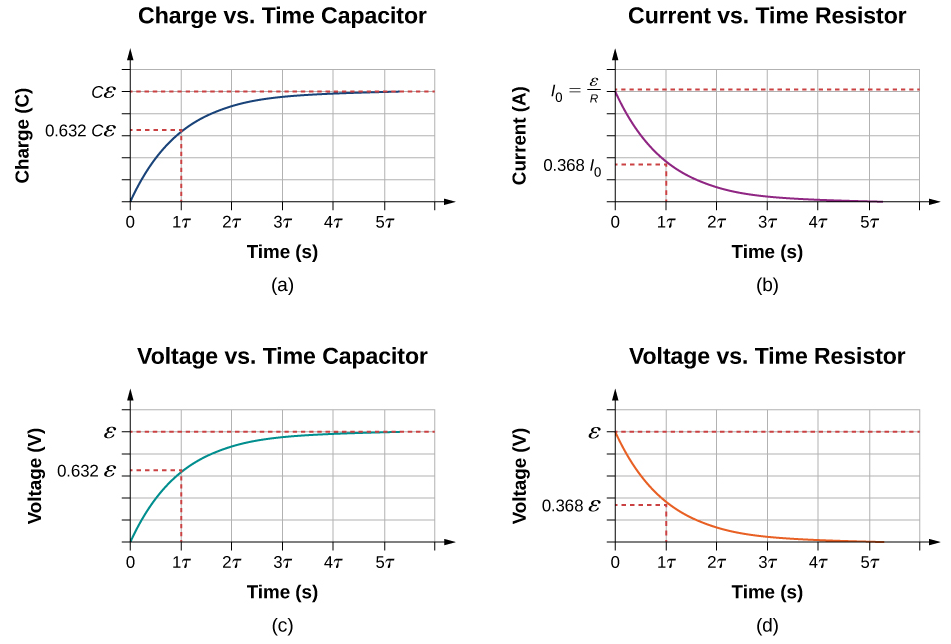
Charge vs Time §

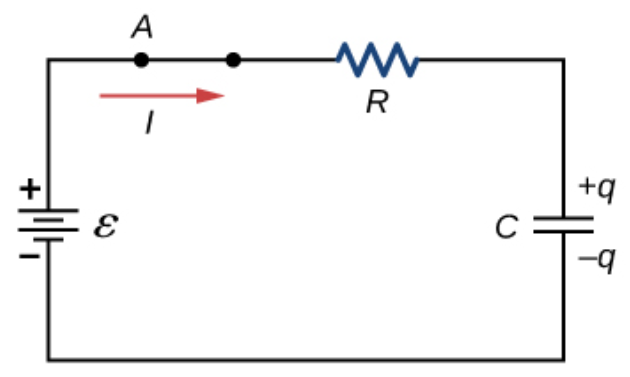
To find the rate at which the capacitor charges, we can use Kirchoff’s Voltage Law, using $ϵ$ as the emf of the battery, $V_R$ as the voltage of the resistor, and $V_C$ as the voltage of the capacitor.

$$\begin{array}{rl}ϵ-V_R-V_C& =0\\ ϵ-IR-\frac{q}{C}& =0\\ ϵ-R\frac{dq}{dt}-\frac{q}{C}& =0\\ \frac{dq}{dt}& =\frac{ϵC-q}{RC}\\ {\int }_0^q\frac{dq}{ϵC-q}& =\frac{1}{RC}{\int }_0^{t}dt\end{array}$$

Using a u-sub for $u=ϵC-q$, we get

$$\begin{array}{rl}-{\int }_0^q\frac{du}{u}& =\frac{1}{RC}{\int }_0^{t}dt\\ \ln \left(\frac{ϵC-q}{ϵC}\right)& =-\frac{t}{RC}\\ \frac{ϵC-q}{ϵC}& =e^{-\frac{t}{RC}}\\ q& =Cϵ\left(1-e^{-\frac{t}{RC}}\right)\end{array}$$

Our final formula for charge as a function of time is

$$\begin{array}{rl}Q& =Cϵ\left(1-e^{-\frac{t}{RC}}\right)\\ & =Q_0\left(1-e^{-\frac{t}{\tau }}\right)\end{array}$$

where $RC$ is also called the time constant, $\tau$.

$V_C$ vs Time §

Since we know that $Q=CV$, $V_C\propto Q$, and therefore

$$\begin{array}{r}{V}_C=V_0\left(1-e^{-\frac{t}{\tau }}\right)\end{array}$$

Current vs Time §

Using the formula for charge as a function of time, we can find the formula for the current running through the resistor as a function of time.

$$\begin{array}{rl}I& =\frac{dQ}{dt}\\ & =\frac{d}{dt}\left[Cϵ\left(1-e^{-\frac{t}{\tau }}\right)\right]\\ & =Cϵ\left(\frac{1}{RC}\right)e^{-\frac{t}{\tau }}\\ & =\frac{ϵ}{R}{e}^{-\frac{t}{\tau }}\\ & =I_0{e}^{-\frac{t}{\tau }}\end{array}$$

Our final formula for current as a function of time is

$$I=I_0{e}^{-\frac{t}{\tau }}$$

$V_R$ vs Time §

Since we know that $V=IR$ , $V_R\propto I$, and therefore

$$V_R=V_0{e}^{-\frac{t}{\tau }}$$

Summary §

Discharging §

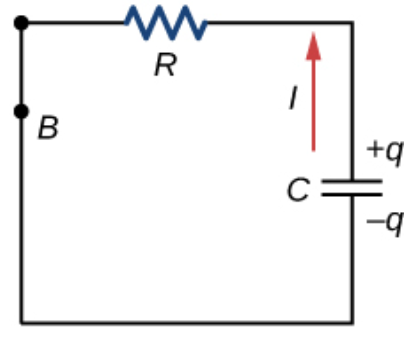
The capacitor discharges until $V_C=0$.

Charge vs Time §

We can use Kirchoff’s Voltage Law again to find charge vs time.

$$\begin{array}{rl}-V_R-V_C& =0\\ -IR-\frac{q}{C}& =0\\ -\frac{dq}{dt}R-\frac{q}{C}& =0\\ \int \frac{dq}{q}& =\int -\frac{dt}{RC}\\ \ln q-\ln Q_0& =-\frac{t}{RC}\\ q& =Q_0{e}^{-\frac{t}{RC}}\end{array}$$

Rewriting, we get that our formula for charge vs time is

$$Q=Q_0{e}^{-\frac{t}{\tau }}$$

Here, $\tau$ is actually the amount of times it takes for the charge to become $\frac{1}{e}$ the amount it was before, kinda like a half-life (but e-life???).

$V_C$ vs Time §

$$V_C\propto Q⟹V_C=V_0{e}^{-\frac{t}{\tau }}$$

Current vs Time §

$$\begin{array}{rl}I& =dQ/dt\\ & =-\frac{Q_0}{\tau }{e}^{-\frac{t}{\tau }}\end{array}$$

$V_R$ vs Time §

$$V_R\propto I⟹V_R=-\frac{V_0}{\tau }{e}^{-\frac{t}{\tau }}$$

Summary §