Particle in a Box Model

Simple but important model that develops physical understanding of chemical applications of quantum mechanics.

One-Dimensional Boxes §

• simplest model problem for which Schrodinger’s Equation can be solved
• particle confined by potential energy barriers with infinite potential energy
  • particle only exists in certain region of box
  • one dimension $⟹$ bead slides along wire between barriers at ends of wires

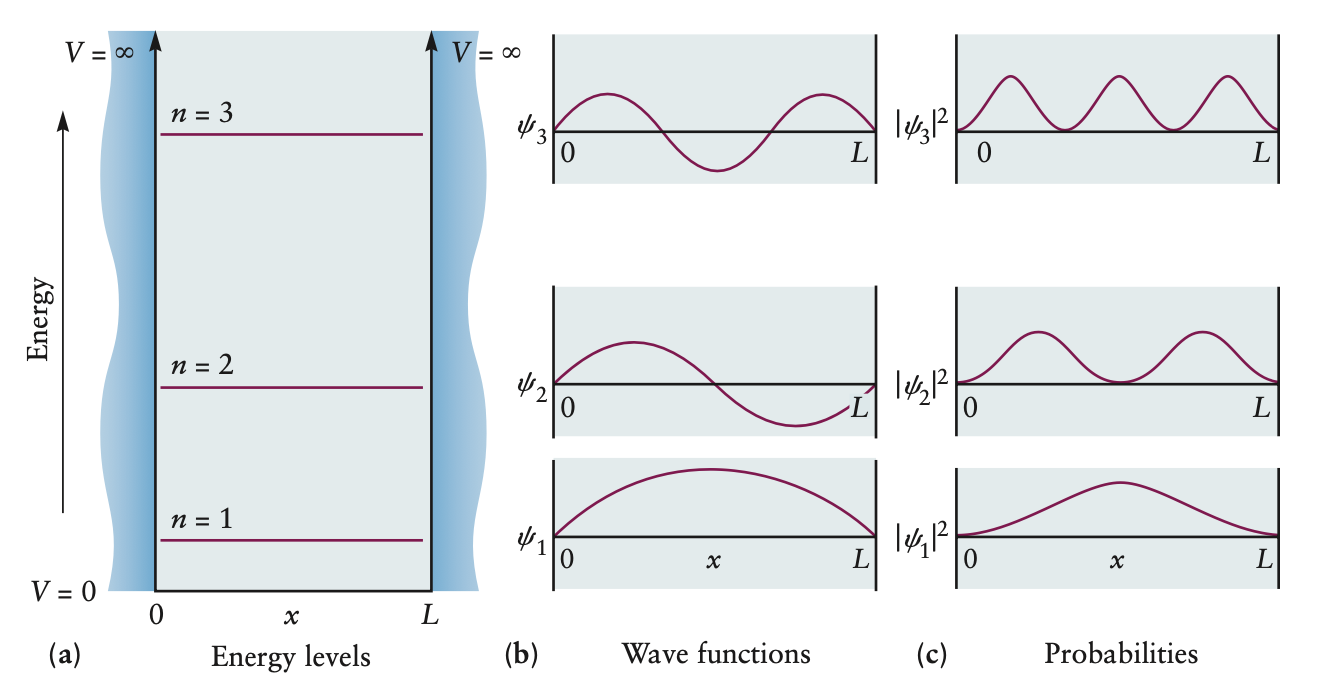
• potential energy inside box is $V(x)=0$, thus
• total energy must be $E=T+V>0$ inside box
• we can use these constraints to solve for all possible energy levels $E$

Since it’s impossible to find particle outside of box,

$$P(x)={\psi }^2(x)=0⟹\psi (x)=0.$$

Inside the box, $V=0$, so Schrodinger’s equation becomes

$$-\frac{h^2}{8{\pi }^{2}m}\frac{d^2\psi (x)}{d{x}^2}=E\psi (x).$$

The LHS is usually simplified with the Hamiltonian operator $\hat{H}$, which gives us the classic

$$\hat{H}\psi =E\psi .$$

Back to the previous equation: we can simplify it to become

$$\frac{d^2\psi (x)}{d{x}^2}=-\frac{8{\pi }^{2}mE}{h^2}\psi (x).$$

Since this is a Linear Differential Equation and our boundary conditions are that $\psi (0)=\psi (L)=0$, we know that

$$\psi (x)=A\sin kx.$$

If $\psi (L)=A\sin kL=0$, then

$$kL=n\pi n=1,2,3,\dots .$$

Thus,

$$\psi (x)=A\sin \left(\frac{n\pi x}{L}\right)n=1,2,3,\dots .$$

Now, we fulfill the normalized property of the wave function:

$$\begin{array}{c}{A}^2{\int }_0^L{\sin }^2\left(\frac{n\pi x}{L}\right)dx=1\\ A^2\left(\frac{L}{2}\right)=1\\ A=\sqrt{\frac{2}{L}}.\end{array}$$

Thus, the normalized wave function for particle in a box is

$${\psi }_n(x)=\sqrt{\frac{2}{L}}\sin \left(\frac{n\pi x}{L}\right)n=1,2,3,\dots$$

where $n$ corresponds to a particular solution for Schrodinger’s Equation.

Solving for energy using ^a2e8ff, we get

$$\frac{d^2{\psi }_n(x)}{d{x}^2}=-{\left(\frac{n\pi }{L}\right)}^2{\psi }_n(x)$$

and

$$\begin{array}{c}-\frac{8{\pi }^{2}m{E}_n}{h^2}{\psi }_n(x)=\frac{d^2{\psi }_n(x)}{d{x}^2}\\ E_n=\frac{n^2{h}^2}{8m{L}^2}.\end{array}$$

The fact that $E$ corresponds to discrete $n$ ties in with the fact that energy is Energy Quantization.